Why does two's complement work?

You probably know that most computers represent negative numbers by taking the two's complement of the corresponding positive number. This allows them to easily do subtraction by addition. You may also know that to find the two's complement of a binary number, all you need to do is flip the bits and add 1 to the result.

If this seems like magic to you and you wonder why it works, read on.

Modular arithmetic

One crucial thing to establish is that we're effectively dealing with modular arithmetic a.k.a. "clock arithmetic".

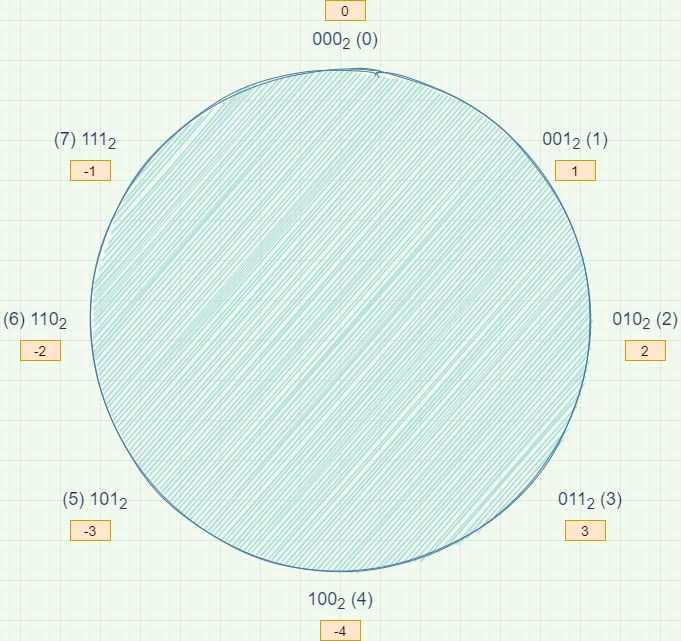
1. Assume we've got only 3 bits to work with. In 3 bits we can represent 2³ = 8 numbers, e.g. the numbers from 0 to 7 (000₂ to 111₂).
2. Let's say we want to represent an equal amount of negative and non-negative numbers in those 3 bits. That gives us the numbers from 0 to 3, and from -4 to -1, all mapped onto what were previously the numbers from 0 to 7 (000₂ to 111₂).

Since we've only got 3 bits to work with, looking at the diagram we can see that adding a multiple of 8 "around the clock" will get us back to the position we started from. We can generalize this for n bits - we will get back to the starting position after adding a multiple of 2ⁿ

It becomes quite clear that subtracting 1 is the same as adding 7, subtracting 2 is the same as adding 6, and so on.

With this mapping it also works out perfectly that adding a number to its negative gives us zero.

In decimal:

2 + -2 = 2 + 6 = 8 = 0; // 8 mod 8 = 0

In binary:

010 + 110 = 1000 = 000; // we only have space for 3 bits, so the 1 gets dropped

Why flipping the bits and adding one gives us the 2's complement?

Using the same scenario as above, how can we find the number -3 if we don't know the algorithm? Simple - we subtract 3 from 0, which is the same as substracting 3 from 8 (remember that every multiple of 8 gives us 0). Here is what this would look like in binary:

1000 - 011 = 1 + (111 - 011) = 1 + 100 = 101;

1000₂ is the same as 1₂ + 111₂.
You should also notice that subtracting a number from 111₂ is the same as flipping the bits of that number.

8-bit example

Let's look at an 8-bit example. We want to find the negative of 72 (01001000₂). This time our "clock" goes to zero every 2⁸ = 256 times, so we need to subtract 72 from 256.

100000000 - 01001000 =
= 1 + (11111111 - 01001000) =
= 1 + 10110111 = 10111000

And that's it.